"Hex Variation" in Haskell
The ReCode aims to re-implement a number of computer artworks in a modern environment. In this case they are using processing to implement the old artworks. I thought it would be a nice task to re-implement one of them in Haskell.
The specific artwork that I liked was called Hex Variation. The algorithm is really very simple. There are three hexagon shapes which all fit together nicely. The three shapes are the same figure but rotated 60 degrees between them.
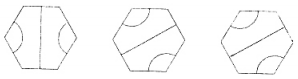
An example of how they can fit together is shown below.
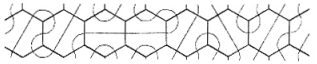
The shapes are then just randomized over a large area to create a quite intriguing pattern.

My haskell implementation is shown below. The program use gloss (a very convenient library to output 2D graphics through OpenGL) to render its graphics. It also uses an infinite list of random numbers.
module Main (main) where
import Graphics.Gloss
import System.Random
type Size = Float -- width and height
type Rs = [Float] -- infinite list of random numbers
h = 1.0 -- hexagon hight (between paralell sides)
s = h*tan(pi/6) -- hexagon side length
-- Draw hexagon at origo. Top, bottom sides are parallel with the x axis. Hexagon height is 1
-- This variant has vertical line through origo and two arcs on the +/- axis
draw_hexagon :: Picture
draw_hexagon = pictures [lt_arc, rt_arc, ln] where
lt_arc = Translate (-s) 0 (Arc (-60) 60 (s/2))
rt_arc = Rotate 180 lt_arc
ln = Line [ (0, (-h/2)), (0, (h/2)) ]
-- Get the locations of all hexagons in the area between (0,0) and (s,s)
get_points :: Size -> [Point]
get_points s' = even_ps ++ odd_ps where
even_ps = [ (x,y) | x <- [0, (3*s) .. (last (3*s) s') ], y <- [0, h .. (last h s') ] ]
odd_ps = map (\(x,y) -> (x + (3*s/2), y + (h/2))) even_ps
last d max = d * (fromIntegral . floor) (max/d) -- last n*d btw. 0 and max
-- Fill area with random hexagons
draw_hexagons :: Size -> Rs -> Picture
draw_hexagons s' rs = pictures hs'' where
ps = get_points s' -- get all target locations
hs = map (\_ -> draw_hexagon) $ take (length ps) [0..] -- create hexagons
hs' = zipWith (\h r -> Rotate r h) hs (take (length ps) rs) -- rotate hexagons randomly
hs'' = zipWith (\h p -> Translate (fst p) (snd p) h) hs' ps -- translate hexagons to ps
-- Draw Hex Variation. Time is currently not used i.e. no animation support
drawHex :: Size -> Size -> [Float] -> Float -> Picture
drawHex s' h rs _ = Translate trans trans $ Scale scale scale $ picture
where
scale = h
trans = -s'/2
picture = draw_hexagons (s'/h) rs
main = do
gen <- getStdGen
let rs = map (fromIntegral . (*60)) $ randomRs (0::Int, 2) gen :: [Float]
display
(InWindow "HexVariation" (600,600) (100,100))
white -- background color
(drawHex 650 50 rs 0) -- picture to display
The program is compiled, optimized and run as follows.
ghc -O2 HexVariation.hs
strip HexVariations -o HexVariationStrip
./HexVariation
Example output from the haskell implementation is shown below.
!(hex_haskell_output)[../files/hex_haskell_output]
You could make up other hexagon symbols to make different patterns.
